名大数学をプログラミングで解く

こんにちは、ひらくと申します。jack 春のブログ祭り4日目です。

アプリ開発団体であるjackですが、最近の私はアプリの開発ではなく、もっぱら競技プログラミングにはまっています。

競技プログラミングでは、参加者全員に同一の課題が出題され、より早く与えられた要求を満足するプログラムを正確に記述することを競う。コンピュータサイエンスや数学の知識を必要とする問題が多く、新卒学生の採用活動などに使われることもある。多くのコンテストでオンラインジャッジが採用されている。（wikipediaより引用）

今回は、新入生の皆さんが解いたであろう今年の名大の数学を、競プロの知識を使ってプログラミングで解いていこうと思います。

使う言語は python です。

ちょうどタイミングよく、前回の記事がpythonの入門をやってくれているので、pythonが分からない方はそちらから読むことをおすすめします。

問題

今回扱うのは、文系数学の大問3です。

問題文でお得意の確率漸化式を匂わせていますが、普通に解くなら確率（と整数）の問題です。

解きたい方は、答えが書いてあるので、事前に解いてから読み進めることをおすすめします。

（１）

裏が $r$ 回出ているということは、表は $n-r$ 回出ているので、最終的な石の位置 $a_n$ は、

と求まります。これはプログラミングを使うまでもないですね。

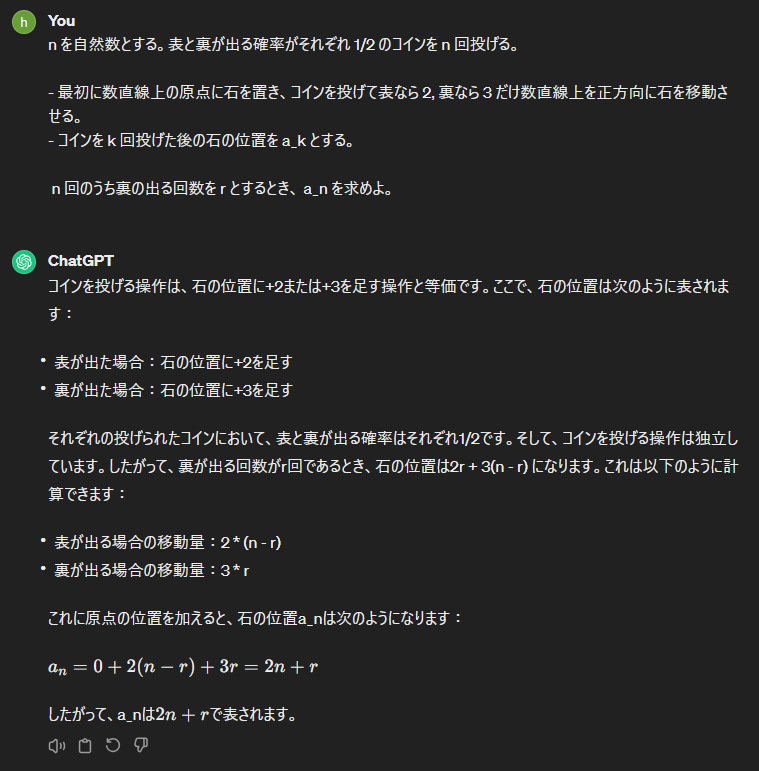
余談ですが、ChatGPTにこの問題を投げたところ、何回かやり直しましたが正解しました。

（２）

これはめんどくさそうなので、シミュレーションしてみましょう。

python では random モジュールを用いて、$0$ 以上 $1$ 未満の乱数を生成することができます。

import random # インポート

for _ in range(5): # ５回生成
  print(random.random())

結果

0.2997763923410265
0.9511662777105855
0.9086456229892494
0.3284149610372963
0.8802635466734381

今回のコイン投げでは、$1/2$ の確率で表か裏が出るので、乱数が $0.5$ 未満なら表、$0.5$ 以上なら裏と対応させることでシミュレーションができます。

具体的には以下のようなコードになります。

n = 4              # コインを投げる回数
iteration = 100000 # 試行回数
count1 = 0         # 得点が0でなかった回数
count2 = 0         # 得点が25になった回数

for _ in range(iteration):
  a = 0     # 石の位置
  score = 0 # 得点

  for i in range(n):
    p = random.random() # 乱数

    if p < 0.5: # p が0.5未満なら表
      a += 2
    else:       # 0.5以上なら裏
      a += 3

    score += a  # 得点に a を足す
  
  if a != 2*n+2: # 石の位置が 2n+2 でないとき、得点は0
    score = 0
  
  if score != 0:  # 得点が0でないときをカウント
    count1 += 1
  if score == 25: # 得点が25のときをカウント
    count2 += 1

print(f"得点が0でない確率は {count1/iteration}, ")
print(f"得点が25である確率は {count2/iteration}. ")

結果

得点が0でない確率は 0.3750141, 
得点が25である確率は 0.1249446. 

答えはそれぞれ $3/8 (=0.375), 1/8(=0.125)$ なので、近い値が得られていることがわかります。

（３）

これも先ほどのシミュレーションの変数や条件式をいじればできそうです。

ですが、先ほどやったのはあくまで確率的なシミュレーションなので、正しい値が求められるわけではありません。

どうせなら厳密な値を求めたいので、今回は動的計画法を使って求めてみましょう。

動的計画法（Dynamic Programming, DP）は、計算機科学の分野において、アルゴリズムの分類の1つである。対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。（wikipediaより引用）

今回の場合、$i$ 回コインを投げたときの状態（石の位置、得点）の確率を管理しておけば、$i+1$ 回コインを投げたときの各状態の確率を求めることができます。

具体的には、以下の画像のように状態が遷移します。（遷移確率はともに $1/2$ です）

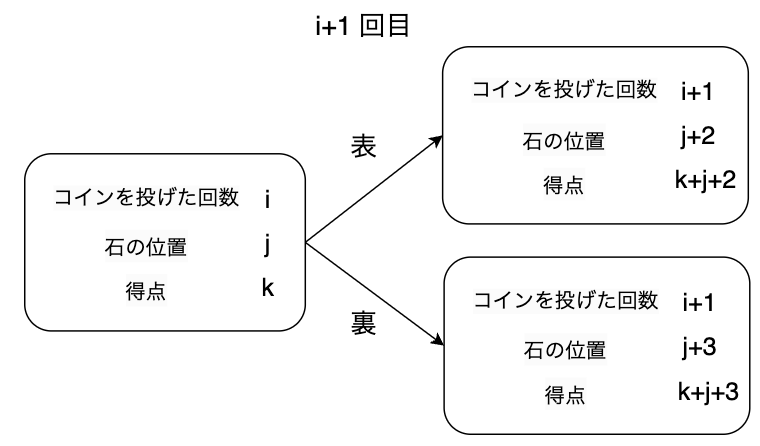
後はこれをコードに落とし込むだけです。

n = 9  # コインを投げる回数

# dp[i][j][k] := i回コインを投げて、石の位置がjであって、得点がkである確率
dp = [[[0]*(200) for _ in range(50)] for _ in range(n+1)]

# 最初は石の位置が0で、得点が0
dp[0][0][0] = 1

for i in range(n):
  for j in range(3*(i+1)+1):
    for k in range(3*n*(n+1)//2+1):

      # i回コインを投げて、石の位置がjであって、得点がkである場合からの遷移を考える

      # i+1回目のコイン投げで表が出た場合,
      # 石の位置は2進み、得点はその時点での石の位置である j+2 が可算される
      dp[i+1][j+2][k+j+2] += dp[i][j][k]*(1/2)

      # i+1回目のコイン投げで裏が出た場合,
      # 石の位置は3進み、得点はその時点での石の位置である j+3 が可算される
      dp[i+1][j+3][k+j+3] += dp[i][j][k]*(1/2)

count1 = 0  # 得点が100である確率
count2 = 0  # 得点が奇数である確率

for j in range(3*n+1):
  for k in range(3*n*(n+1)//2+1):

    if j == 2*n+2 and k == 100: # 得点が100であるときをカウント
      count1 += dp[n][j][k]

    if j == 2*n+2 and k%2 == 1: # 得点が奇数であるときをカウント
      count2 += dp[n][j][k]


print(f"得点が100である確率は {count1}, ")
print(f"得点が奇数である確率は {count2}. ")

結果

得点が100である確率は 0.0078125, 
得点が奇数である確率は 0.0390625. 

答えはそれぞれ $1/128 (=0.0078125), 5/128(=0.0390625)$ なので、正しい値を求めることができました！！！

さいごに

今回は今年の名大の数学をプログラミングで解いてみました。

jackに興味がある方、今回の記事や競技プログラミングに興味を持った方は、ぜひ新歓に遊びに来てください！（詳細は jackのX をご確認ください）

また、今回作成したコードはここにあります。コピーしていろいろ遊んでみてください。

では、明日以降の記事もお楽しみに～